4.4. Confidence-based properties on COMPAS¶

4.4.1. Use case presentation¶

COMPAS is a neural network that, based on a selection of features such as gender and race, assesses the probability of criminal defendants committing future crimes [1].

The neural network that is used is a feedforward neural network with 6 inputs, 3 outputs, and 2 hidden layers composed of 5 neurons each (available at examples/confidence_properties/nnet/compas.nnet ).

4.4.2. Properties¶

The idea of confidence-based safety properties is to add a constraint to the original safety property of interest: the confidence score \(\text{conf}\) of the input considered in the property must be above a given threshold \(\kappa\). This notion is also applicable to global safety properties such as global robustness or global fairness. A neural network \(f:\mathbb{R}^n\rightarrow\mathbb{R}^m\) is globally safe for confidence \(\kappa\in]0,1]\) if and only if \(\forall \mathbf{x},\mathbf{x}'.P(\mathbf{x},\mathbf{x}')\land\text{conf}(f(\mathbf{x}))>\kappa\Rightarrow Q(\mathbf{x},\mathbf{x}')\), where \(P\) and \(Q\) are the respective precondition and postcondition of the global safety property.

In CAISAR, it is possible to verify the confidence-based gobal robusness of a model. A neural network \(f:\mathbb{R}^n\rightarrow\mathbb{R}^m\) is globally \(\varepsilon\)-robust for confidence \(\kappa\in]0,1]\) if and only if \(\forall \mathbf{x},\mathbf{x}'.||\mathbf{x}-\mathbf{x}'||\leq\varepsilon\land\text{conf}(f(\mathbf{x}))>\kappa\Rightarrow\text{class}(f(\mathbf{x})) = \text{class}(f(\mathbf{x}'))\), where \(\varepsilon>0\) and \(||\cdot||\) is the distance metric over the input space of the neural network \(f\).

The concept of confidence-based global robustness is illustrated here:

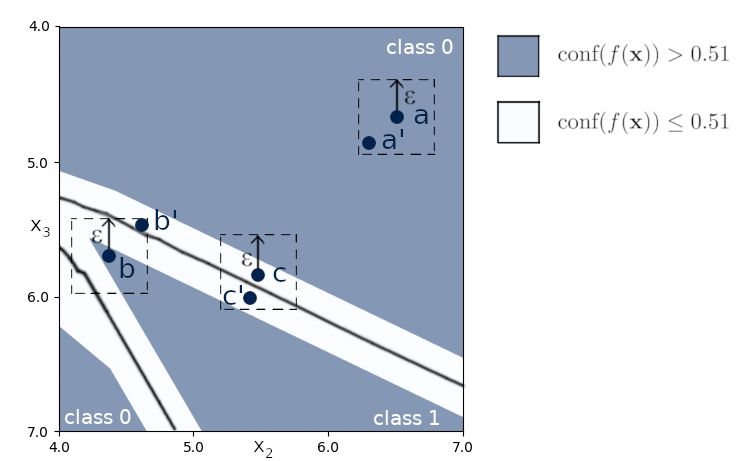
In this figure, \(||\mathbf{c}-\mathbf{c}'||\leq\varepsilon\), \(||\mathbf{a}-\mathbf{a}'||\leq\varepsilon\) and \(||\mathbf{b}-\mathbf{b}'||\leq\varepsilon\). Since \(\text{conf}(f(\mathbf{c}))\leq0.51\) and \(\text{conf}(f(\mathbf{c}'))\leq 0.51\), \((\mathbf{c},\mathbf{c}')\) is not a counterexample for global robustness with confidence, even if \(\text{class}(f(\mathbf{c}))\neq\text{class}(f(\mathbf{c}'))\). Same remark for \((\mathbf{a},\mathbf{a}')\) since \(\text{class}(f(\mathbf{a}))=\text{class}(f(\mathbf{a}'))\). However, \(\text{conf}(f(\mathbf{b}))>0.51\) and \(\text{class}(f(\mathbf{b}))\neq\text{class}(f(\mathbf{b}'))\): \((\mathbf{b},\mathbf{b}')\) is a counterexample and therefore \(f\) is not globally robust with confidence \(\kappa=0.51\) and tolerance \(\varepsilon\).

The confidence metric can be defined and chosen by the user. For now, CAISAR proposes to use a confidence metric based on applying a softmax layer to the last layer of the neural network.

4.4.3. Modelling the problem using WhyML¶

As described for the example on Functional properties of ACAS-Xu and (Local) Robustness of MNIST dataset, we first need to write a specification file containing a WhyML theory to describe the verification problem.

The CAISAR standard library provides theories for the specification of confidence-based properties (caisar.confidence.ClassGlobalRobustConf and caisar.confidence.ConfidenceMeasure). Most predicates are taken from these theories.

We start by importing all necessary theories.

use ieee_float.Float64
use caisar.model.Model
use caisar.types.IntWithBounds as Label
use caisar.types.Vector
use caisar.types.VectorFloat64 as FeatureVector
use caisar.confidence.ClassGlobalRobustConf
use caisar.confidence.ConfidenceMeasure

We introduce constants that will be defined by the user on the command line at the time of executing CAISAR.

constant model_filename: string
constant eps: Float64.t
constant threshold: Float64.t

As COMPAS has three output classes, we specify the bounds of the label as follows.

constant label_bounds: Label.bounds =
  Label.{ lower = 0; upper = 2 }

The input variables of this neural network have different bounds. To check them, the user has to specify the input bounds of each component. To do so, the user has to define a generic type bounds as follows.

type bounds = {
  b0: Float64.t;
  b1: Float64.t;
  b2: Float64.t;
  b3: Float64.t;
  b4: Float64.t;
  b5: Float64.t
}

Then, the user can specify the input bounds of the model, using this type.

constant lbounds: bounds = {
  b0 = (0.0:t);
  b1 = (0.0:t);
  b2 = (0.0:t);
  b3 = (0.0:t);
  b4 = (1.0:t);
  b5 = (0.0:t)
}
constant ubounds: bounds = {
  b0 = (1.0:t);
  b1 = (8.0:t);
  b2 = (1.0:t);
  b3 = (6.0:t);
  b4 = (4.0:t);
  b5 = (2.0:t)
}

Using these constants, the user can define a predicate for checking the validity of input bounds.

predicate valid_input_bounds (x: FeatureVector.t) =
  (x[0] .>= lbounds.b0 /\ x[0] .<= ubounds.b0) /\
  (x[1] .>= lbounds.b1 /\ x[1] .<= ubounds.b1) /\
  (x[2] .>= lbounds.b2 /\ x[2] .<= ubounds.b2) /\
  (x[3] .>= lbounds.b3 /\ x[3] .<= ubounds.b3) /\
  (x[4] .>= lbounds.b4 /\ x[4] .<= ubounds.b4) /\
  (x[5] .>= lbounds.b5 /\ x[5] .<= ubounds.b5)

The user can now formalize the verification goal using this predicate and the ones defined in the confidence-based theories.

goal conf_global_robustness:
  let nn = read_model model_filename in
  let len = 6 in
  let bounds = (fun x -> valid_input_bounds x) in
  let conf_measure = (fun m x -> softmax_confidence m x) in
  confidence_globally_robust bounds
                             label_bounds
                             lbounds
                             ubounds
                             len
                             nn
                             eps
                             threshold
                             conf_measure

confidence_globally_robust is a predicate defined in caisar.confidence.ClassGlobalRobustConf and implements the property of confidence-based global robustness.

The confidence measure is given by conf_measure and is selected from the caisar.confidence.ConfidenceMeasure theory. Currently, only softmax_confidence, the confidence measure based on the softmax layer, is available.

4.4.4. Verifying the property with CAISAR¶

For now, only two provers are able to verify confidence-based global robustness in CAISAR: PyRAT and Maraboupy. It can be done as follows:

$ caisar verify -p PyRAT --prover-altern confidence -m:16GB -t:60s --define eps:1.0 --define threshold:0.5 --define model_filename:nnet/compas.nnet examples/confidence_properties/compas.why
[caisar] Goal conf_global_robustness: Invalid

Maraboupy has a small internal issue that is fixed by asking specifically CAISAR not to use \(\texttt{Sub}\) ONNX nodes in the reformulation of an operator. It is currently done by using the environment variable CAISAR_CLIP_ADD_ONLY:

$ export CAISAR_CLIP_ADD_ONLY=TRUE && caisar verify -p maraboupy -t:60s --define eps:1.0 --define threshold:0.5 --define model_filename:nnet/compas.nnet examples/confidence_properties/compas.why
[caisar] [WARNING] Clip rewriting: all Sub operators are expressed using Add operators
[caisar] Goal conf_global_robustness: Unknown ()

CAISAR states here that there exist a classification change for the given confidence threshold of \(0.5\) and a neighborhood of \(1.0\). It is no surprise, given that a softmax output of \(0.5\) is rather low for 3 classes, and that the distance between the two inputs is very high. Indeed, as we have defined previously, the first coordinate of the input lies within \(0\) and \(1\). By specifying such a high value for \(\epsilon\), we cover an input neighborhood that will possibly cross the decision boundary.

By being more conservative on the input neighborhood and the confidence score, we can prove the property valid.

$ export CAISAR_CLIP_ADD_ONLY=TRUE && caisar verify -p maraboupy -t:60s --define eps:0.001000000047497451305389404296875 --define threshold:0.89999997615814208984375 --define model_filename:nnet/compas.nnet examples/confidence_properties/compas.why
[caisar] [WARNING] Clip rewriting: all Sub operators are expressed using Add operators
[caisar] Goal conf_global_robustness: Valid

Here, we are able to prove that on a sufficiently small neighborhood and a high confidence, the classification does not change.